Counting matchings in cycle graphs
How many distinct matchings does a labeled cycle graph of $n$ nodes have?
Last July, Melanie and I taught in a training camp for beginners in programming competitions. In one of the days, we put a problem in the daily contest called Edge Cases, which was basically the following: how many distinct matchings does a labeled cycle graph of $n$ nodes have? Just a quick recap: a matching is a set of edges such that no two of them share an endpoint (or, more intuitively, a way of grouping vertices into pairs, so that there's an edge between each pair and no vertex belongs to more than one pair). We're going to use $C_n$ to denote a labeled cycle of $n$ vertices.
Expected solution - a simple dynamic programming
We expected a simple dynamic programming solution. The tricky part is the cycle, which can be easily broken by considering two cases. Suppose vertices are labeled from $v_1$ to $v_n$. Let's consider vertices $v_1$ and $v_n$. There are matchings that contain the edge $(v_1, v_n)$, and matchings that do not. If we match up vertices $1$ and $n$, we now have to form a matching of the path between vertices $v_2$ and $v_{n-1}$. If we do not, then we can remove the edge $(v_1, v_n)$ from the graph, and form a matching of what remains, which is the full path between $v_1$ and $v_n$. If we know how to compute the function $f(n)$ which gives the number of distinct matchings of a path of $n$ nodes, then the answer to our problem is $c(n) = f(n-2) + f(n)$.
Now, $f(n)$ can be computed by a simple recurrence. We can either match the first two vertices in the path or not. If we do, we have to match the remaining path of $n-2$ vertices; if we do not, we are left with a path of $n-1$ vertices. Thus, $f(n) = f(n-2) + f(n-1)$. The base cases are trivial: $f(0) = f(1) = 1$ (only the empty matching is possible in both cases). We then compute $f$ with dynamic programming, and with that compute the answer $c(n)$ to the problem by adding our "fix" to make it work in the circular case.
A pattern (a.k.a. solving the problem without knowing what you're doing)
One team in the training camp didn't see this, but still found a solution to the problem. They noted a simple pattern in the first values of $c(n)$ (let's assume $n \geq 3$ to make visualizing the cases simpler):
- $c(3) = 4$ (we can either pick exactly one of the 3 edges, or none)
- $c(4) = 7$
- $c(5) = 11$
- $c(6) = 18$
You can get to these values by filling a few sheets with drawings. In many problems, analyzing small cases does not help that much in finding a pattern, and you really have to understand what's going on to come up with a solution. But in this case, they noted that, apparently, maybe $c(n) = c(n-1) + c(n-2)$. It turned out that this solution was actually correct.
Satisfied?
If you minimally appreciate the beauty often hidden in mathematical truths, just noticing that $c(n) = c(n-1) + c(n-2)$ works for small cases and getting "Accepted" on the online judge isn't enough. In fact, we also managed to derive this recurrence from our relation between $f$ and $g$, but a purely algebraic proof that doesn't give any intuition is still not appealing. In the path case it is quite intuitive, but it isn't obvious at first how the number of matchings in a cycle of $n$ vertices connects to the number of matchings in a cycle of $n-1$ and $n-2$ vertices. So we tried to prove this afterwards, and well, I thought it was worth it posting the proof (although it's surely a known fact to the academic community, but it's more fun when you get the result yourself :) ). So here it goes.
Theorem: If $n \geq 5$ and g(n) is the number of matchings of $C_n$, then g(n) = g(n-1) + g(n-2)
Proof. Let $M_i$ be the set of matchings of a labeled cycle of $i$ nodes. We are going to show a bijection between $M_i$ and $M_{i-1} \cup M_{i-2}$. Since $M_{i-1}$ and $M_{i-2}$ are obviously disjoint (they are matchings of different graphs), from this bijection we get $|M_i| = |M_{i-1}| + |M_{i-2}|$, which proves what we want.
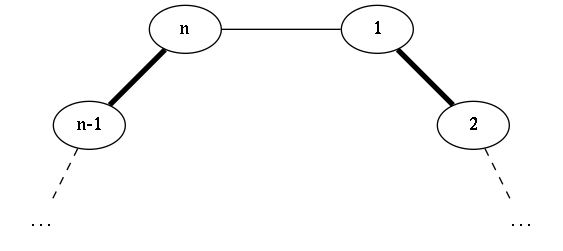
Let's consider matchings of a cycle of $n$ nodes. If we consider vertices $n-1$, $n$, $1$ and $2$, we have 5 possible cases (thicker edges are those in the matching):
Case 1:
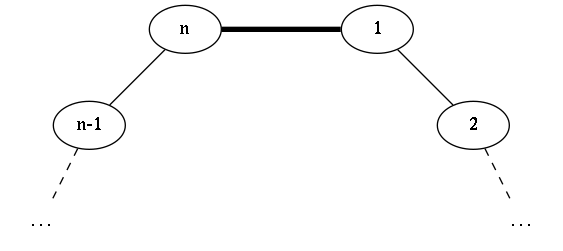
Case 2:
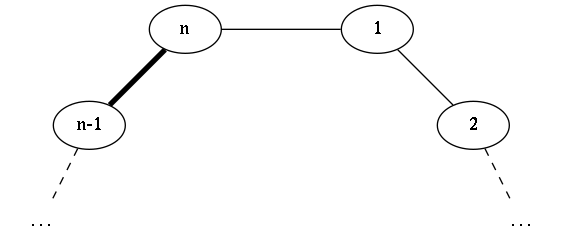
Case 3:
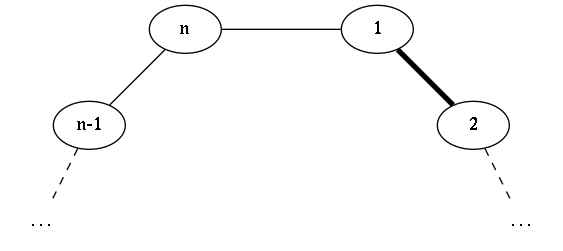
Case 4:
Case 5:
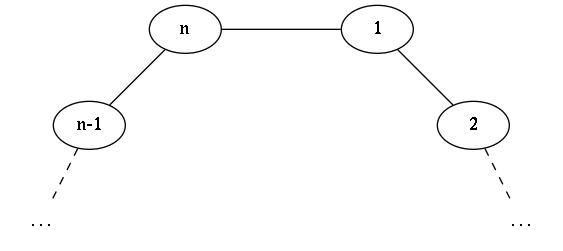
We're going to show that matchings that fall into cases $1$ and $2$ correspond 1:1 to matchings of a cycle of $n-2$ vertices, whereas cases $3$, $4$ and $5$ correspond to matchings of a cycle of $n-1$ vertices.
Let's start with cases $1$ and $2$. Let's add an imaginary edge between vertices $v_{n-1}$ and $v_2$. With this edge, we can see that vertices $v_2$ to $v_{n-1}$ form a cycle of size $n-2$. For each matching in this smaller cycle, the edge between $v_2$ and $v_{n-1}$ can either be in it or not.
If that edge is in the matching of $C_{n-2}$, we can construct a matching in $C_n$ where all edges except that one (between $2$ and $n-1$) are kept, but in $C_n$ the edges $(v_{n-1}, v_{n})$ and $(v_1, v_2)$ are in the matching. The converse is also true: if we have a matching in $C_n$ that has edges $(v_1, v_2)$ and $(v_{n-1}, v_{n})$, we can build a matching of $C_{n-2}$ where the vertices corresponding to $v_2$ and $v_{n-1}$ are matched.
On the other hand, if our imaginary edge between $v_2$ and $v_{n-1}$ is not in the matching of $C_{n-2}$, then we can build a matching in $C_n$ where $v_1$ and $v_n$ are matched.
The following images summarize this argument:
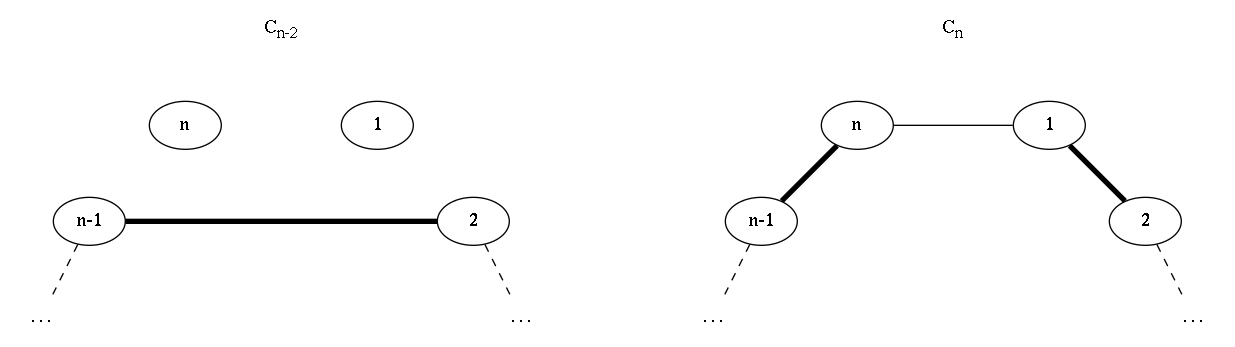
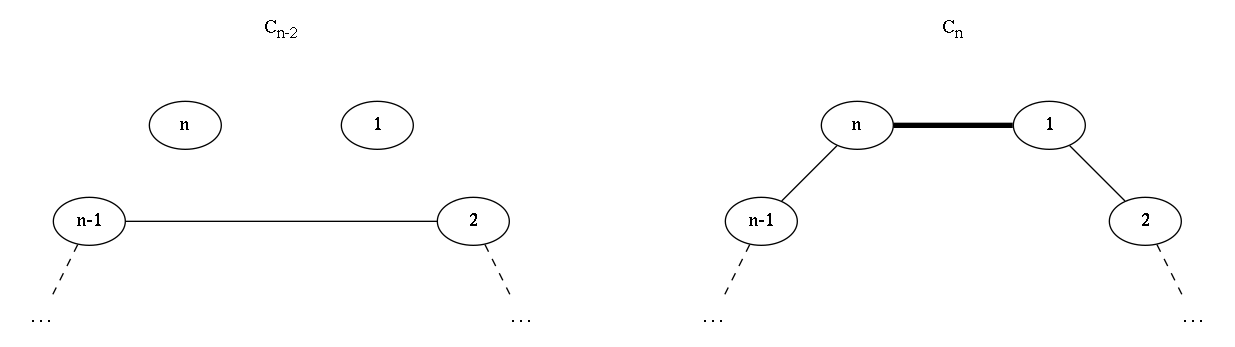
Right, so matchings in $C_{n-2}$ that contain the "top edge" correspond to matchings in $C_{n}$ that fall in our case 1. Matchings in $C_{n-2}$ that do not contain that edge map to matchings in $C_n$ in our case 2. We're left with 3 other cases (we're almost there, this shall be quick).
Now let's create an artificial vertex $v_a$, that connects to $v_2$ and $v_{n-1}$. Notice that $v_a, v_2, \cdots, v_{n-1}$ form a cycle of size $n-1$. Let's consider all matchings of this cycle, and look at $v_{n-1}$, $v_a$ and $v_2$. We have three possible cases for the edges between these three vertices (and, remarkably, three cases left in our proof :-) ):
-
$v_{n-1}$ and $v_a$ are matched. In this case, we construct a matching in $C_n$ where $v_{n-1}$ and $v_{n}$ are matched (and the rest is kept as it was) (our case 3).
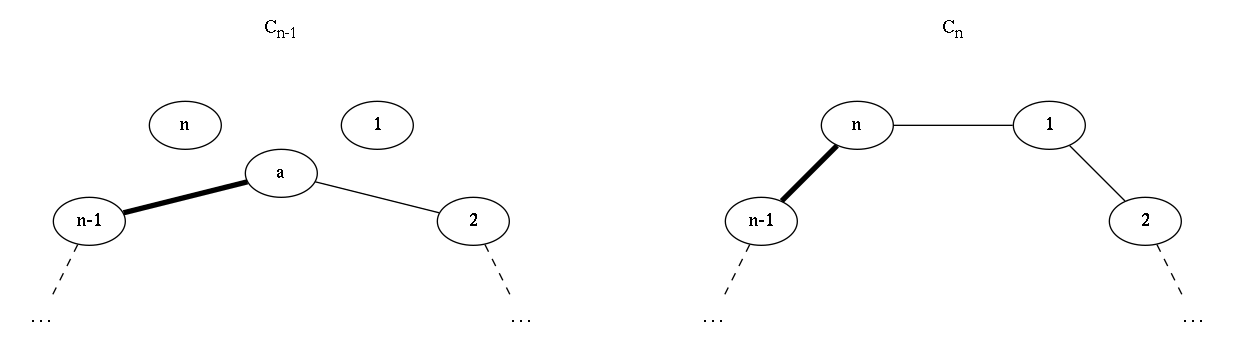
-
$v_{a}$ and $v_2$ are matched. If so, we can construct a matching in $C_n$ where $v_{1}$ and $v_{2}$ are matched, keeping the rest (our case 4).
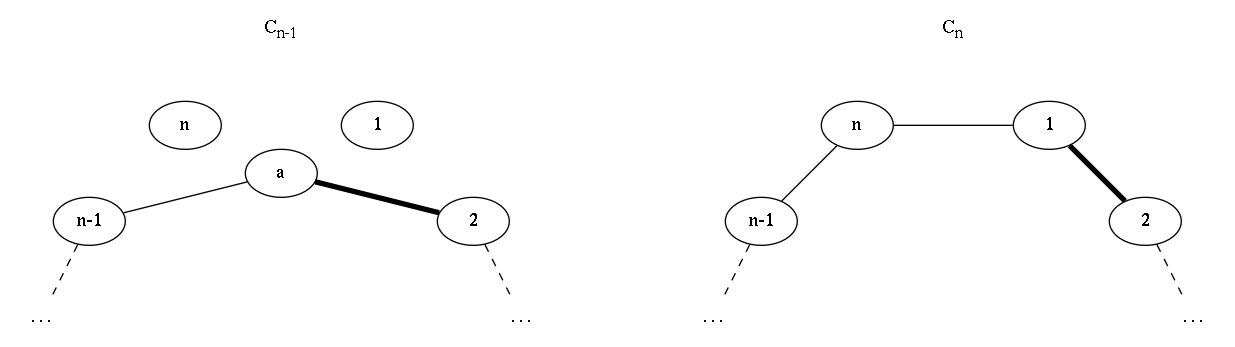
-
Neither $(v_{n-1}, v_a)$ nor $(v_a, v_2)$ are in the matching. Finally, this case maps to the case in which $v_1$ and $v_n$ are both outside of the matching (our case 5).
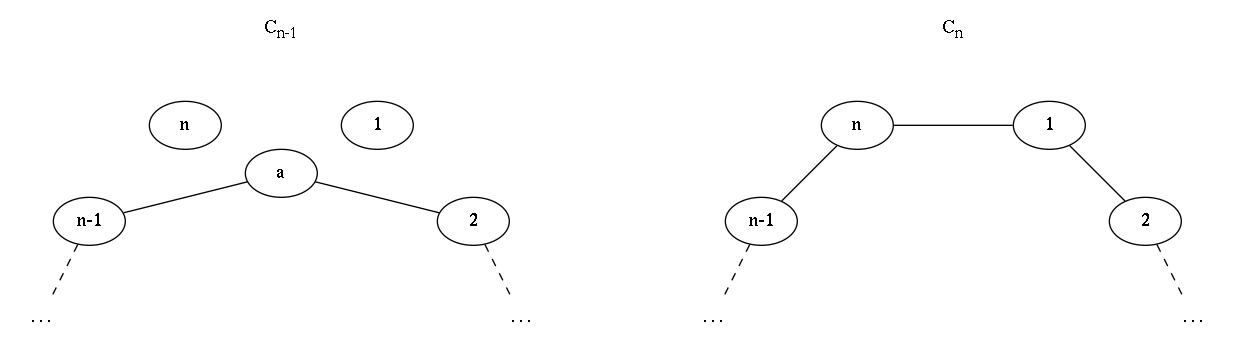
It's easy to see that the opposite is also true: from cases 3, 4 and 5 of matchings in $C_n$, we can find corresponding matchings in $C_{n-1}$ (i.e. in the images, we can go from right to left or from left to right).
Thus, $|M_n| = |M_{n-1}| + |M_{n-2}|$. $$\tag*{$\blacksquare$}$$